Marketing involves a series of critical decisions, each with numerous possible options: Should you invest in branded search? On which TV channels should you run your ads? To decode the vast amounts of data generated by marketing activities, businesses often turn to Marketing Mix Models (MMM). These models aim to attribute the effects of various media channels to key performance indicators (KPIs) such as sales.
However, traditional MMMs, while effective, have limitations, particularly in how they handle sparse data and complex marketing environments. In this article, we’ll explore how extending MMMs with advanced statistical methods can offer a more accurate and insightful view of your marketing efforts.
The Challenge of Traditional MMMs
Most MMMs rely on multiple linear regression models, rooted in Frequentist statistics. These models typically use Maximum Likelihood Estimation (MLE) to find the best-fit relationship between media spend and sales. However, there’s a key challenge: the number of variables we want to model often exceeds the available data points (i.e., time entries). Additionally, marketing data is frequently sparse, as media spend — especially on channels like TV — may be zero for many days.
This imbalance between variables and data points leads to overfitting.
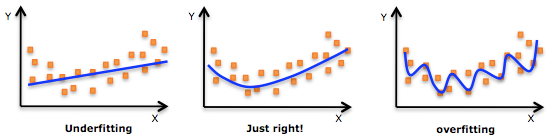
Overfitting occurs when a model becomes too good at predicting the training data, but loses its ability to generalize to new, unseen data, rendering the model unreliable for future predictions.
Overcoming Overfitting with Bayesian Statistics
Fortunately, there’s a powerful solution to overfitting: Bayesian statistics, specifically Bayesian hierarchical modeling. This approach allows us to incorporate domain knowledge directly into the model, creating more robust and reliable predictions. For example, we can encode assumptions like “a media channel should have a positive ROI” or “macroeconomic factors shouldn’t account for more than 10% of sales.” By embedding these reasonable constraints, we can avoid overfitting and improve the model’s real-world relevance.
Additionally, Bayesian models allow us to pool information across variables. If we assume that similar TV channels—such as Discovery 1 and Discovery 2—will produce comparable responses to the same media ads, we can incorporate this assumption to strengthen the model’s ability to handle sparse data.
Quantifying Uncertainty with Posterior Distributions
Another advantage of Bayesian modeling is the ability to generate a posterior distribution over model parameters. Unlike traditional models that offer point estimates, Bayesian models give us a probability distribution for each parameter, providing more nuanced insights into the uncertainty surrounding the model’s predictions.
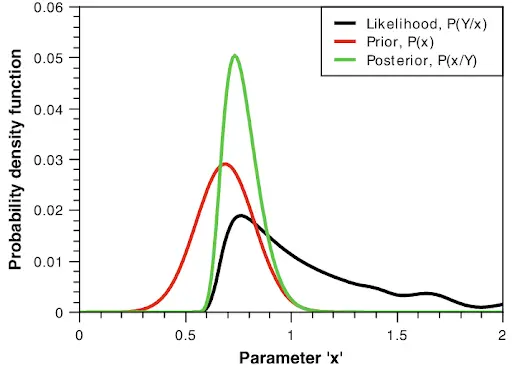
For example, if you’ve only run ads on a TV channel for five days, the model will rightfully express a high degree of uncertainty about the channel’s ROI. On the other hand, if you’ve been advertising on the same channel for years with consistent results, the model will be much more confident in its ROI estimates. This kind of uncertainty estimation is crucial for making informed decisions, particularly when dealing with sparse or incomplete data.
Adstock: Modeling the Decay of Advertising Effects
One of the most crucial components in MMMs is capturing the adstock effect — the idea that the impact of an advertisement doesn’t occur entirely on the day it runs, but rather, its influence “decays” over time. The way we model adstock has a significant impact on how accurately we can attribute sales to media spend.
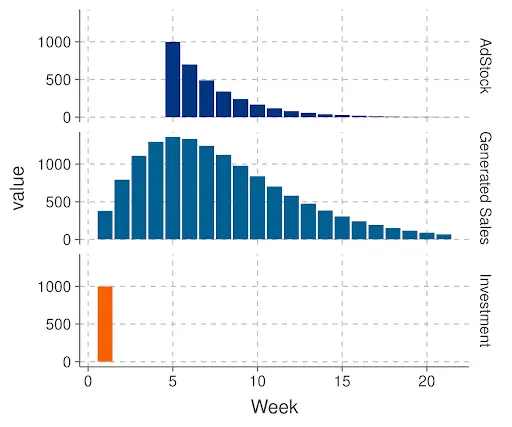
Traditional Adstock
The traditional adstock model assumes that the greatest effect of an ad occurs on the same day it airs, with the impact decaying rapidly afterward. This assumption works well in some cases but can be wildly inaccurate in others. For example, if an ad runs late on a Friday night, but the store being advertised is closed until Monday, the peak effect won’t happen immediately.

Delayed Adstock
To address this, marketers have developed delayed adstock models, which shift the peak effect slightly into the future. However, these models still assume a sharp peak, followed by rapid decay, which doesn’t account for the more gradual and varied ways consumers respond to advertising.
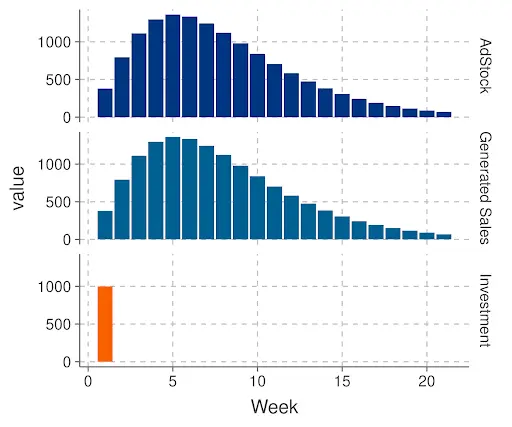
Advanced Adstock
In reality, the effect of advertising is often more complex, requiring models that allow for both ramp-up and ramp-down behavior. Different consumers react at different times, depending on factors like personal schedules and buying intent. Advanced adstock models are designed to capture this nuanced response, offering a more accurate view of how ads drive sales over time.
Bayesian Modeling and Real-World Dynamics
At the heart of these advanced modeling techniques is Bayesian hierarchical modeling. It not only improves predictions and reduces overfitting, but it also helps capture the complex dynamics that drive real-world business outcomes. Whether you’re measuring the long-term impact of TV ads or the immediate effect of online campaigns, a well-constructed Bayesian model can handle the intricacies of diverse media channels and customer behaviors.
Conclusion: Enhancing Your Marketing with Advanced MMMs
By extending traditional MMMs with Bayesian hierarchical modeling and improved adstock functions, businesses can gain a deeper, more accurate understanding of how their marketing efforts drive sales. These extended models not only help to avoid the pitfalls of overfitting, but they also provide meaningful insights into the uncertainty and dynamics of marketing investments.
If you’re ready to take your marketing analytics to the next level, modern tools can integrate Bayesian principles to give you a more complete picture of your marketing performance, enabling better decision-making for future campaigns.